A raíz de publicaciones anteriores donde reflexionaba acerca de los diferentes algoritmos que existen para resolver las operaciones aritméticas básicas, quedó pendiente profundizar más en el caso de las sumas con llevadas.
Una cosa que me llama la atención es que la forma en la que se aborda su tratamiento en los diferentes documentos que regulan el currículo. Por ejemplo, en el decreto que lo regula en la Comunidad Valenciana, en relación al primer curso de primaria aparece como "Utilización de los algoritmos escritos de suma llevando y sin llevar y resta sin llevar. "
En este caso, y si nos centramos en la suma llevando, podríamos preguntarnos si lo que el decreto expresa hace referencia a que hay que enseñar a los alumnos a resolver determinadas sumas con un algoritmo concreto o que, en cambio, lo que hay que hacer es enseñarles a resolver cualquier tipo de sumas empleando los algoritmos que sirvan a ello. Me explico a continuación.
Cuando realizamos una suma sencilla, como esta, seguimos una serie de pasos bien conocidos
Primero, operamos verticalmente empezando por las unidades
Una vez completado este paso, realizamos lo mismo en la columna de las decenas
En este caso, la forma de operar que hemos aplicado anteriormente nos plantea una situación inesperada, dado que al sumar 4 + 7 no podemos simplemente escribir el resultado en la parte inferior de la columna
Esta forma de abordar la suma nos brindaría una solución incorrecta, 311. Así pues se hace necesario un algoritmo (un conjunto de instrucciones) diferente que nos permita alcanzar la respuesta correcta. En ese contexto, y sirviéndonos del valor posicional de las cifras, conocemos que la cifra 1 a la izquierda de 11 es una decena y que, cómo tal, podemos agruparla con el resto de decenas que aparecen en la operación. Hay varias formas de hacerlo.
La primera, y la más habitual, es colocar la decena obtenida en la suma parcial, en la columna siguiente, junto con el resto y completar la operación.
Otra forma de hacerlo es hacer las sumas parciales de cada columna y posteriormente sumar todas las decenas obtenidas
La dinámica es la misma, lo único que cambia es la forma en la que almacenamos temporalmente las decenas parciales. Sea como sea, esta forma de reagrupar las decenas parciales es lo que conocemos como "llevadas" ya que se "llevan" a la columna correspondiente y allí se añaden al resto.
No obstante esta suma puede afrontarse de una manera bien distinta si hacemos uso de los algoritmos abn, "algoritmos abiertos basados en números", que se basan en el trabajo sobre las cantidades en lugar de las cifras.
En primer lugar, la construcción del concepto de número explora con muchas más profundidad sus posibilidades internas. De este modo 24 no solo es 20 + 4 sino 20 + 1 + 1 + 1 +1 y 20 + 3 + 1 y 10 + 10 + 2 + 2, etc. Esto significa que cuando manejamos un número no sólo lo hacemos de una forma cerrada y fija sino que nos sentimos libres como para hacer uso de cualquiera de sus posibles configuraciones. Se dedica tiempo a manejar con soltura las posibilidades combinatorias para formar 10, 100, etc.
En segundo lugar, y también en relación al primer apartado, lo que sumamos son cantidades, números, no cifras aisladas. Así pues, en la suma anterior, no sumaríamos 2 y 1 como cifras que representan la decenas sino que sumaríamos 20 más 10.
Teniendo en cuenta estas dos cuestiones, la suma de cantidades y las posibles descomposiciones de un número, los algoritmos abn nos ofrecen infinidad de opciones para resolver una misma operación. De ahí la denominación de "abiertos".
Por ejemplo:
24+17
Sumamos 24+10 unidades de las 17 que hay en el segundo sumando.
quedarían 34 y 7
Sumamos 34 y 6 unidades de las 7 que hay en el segundo sumando para completar 10 más.
quedaría 40 y 1 unidad
Resultado final: 41
La representación gráfica sería algo así:
Sin embargo, abn permite al alumno realizar la operación descomponiendo los sumandos según su propia madurez o su criterio de comodidad. De este modo, la misma operación podría resolverse también de la siguiente manera:
Como decía antes, cada alumno elige la estrategia más adecuada para resolver la operación y, a medida que mejora su dominio de las cantidades y sus posibilidades combinatorias se reduce el número de pasos necesarios para alcanzar la solución.
De hecho, si la madurez del niño le permite hacer mentalmente sumas más grandes que la decena, puede hacerlas perfectamente. Abn no le impide hacer este tipo de sumas, simplemente no establece una forma cerrada y única de resolver las operaciones.
Explicada esta forma de abordar la suma, me gustaría retomar el planteamiento inicial de la entrada. El decreto que establece el currículo habla de "Utilización de los algoritmos escritos de suma llevando y sin llevar y resta sin llevar." , sin embargo el algoritmo abn resuelve la suma sin necesidad de emplear el recurso de las llevadas. Repito: No hay llevadas porque no hay decenas fruto de una suma parcial que deban guardarse para una suma parcial posterior.
Así pues, cuando el decreto establece ese contenido, es lícito preguntarse si lo hace en base a considerar que sólo hay un algoritmo válido (el que precisa de las llevadas y que se basa en el uso de las cifras) para resolver ese tipo de sumas o si, en realidad, lo que plantea es la necesidad de poder resolver cualquier tipo de suma y el tipo de algoritmo utilizado es secundario.
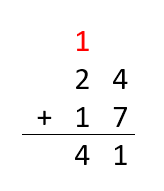
No hay comentarios:
Publicar un comentario